nuke教程之色彩空间原理精讲(八)
02.Exponential Math [指数运算]
Gamma虽然是 一个专有名词,其实可以解释为power (指数)运算。如果参数x的Gamma值为a,那么这个公式可以写为:
y=xa
我们通常将X称为底数,a称为指数。需要记住的就是这样的一个公式:
output = inputGamma
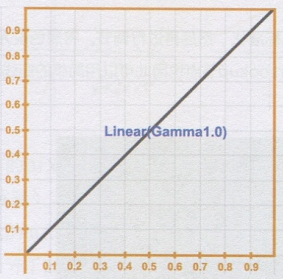
Power指数函数对于读者来说可能不是很直观,但其实它很简单。只需要把底数设置为0~1,如果指数设置为1,那么结果就不会改变(恒等公式),比如图中的“Gammal 0曲线”这时当我们把指数设置为2,也就是底数的平方。通过这样的操作,我们会得到一些很重要的特性:
0.002= 0.00●0.00=0
0.252= 0.25●0.25 = 0.0625
0.502= 0.50●0.50= 0.25
0.752 = 0.75●0.75= 0.5625
1.002= 1.00●1.00= 1.00
请注意,图中 的Gamma2.0曲线,在这个例子中我们可以看到当指数大于1时最终的结果要小于输入值。
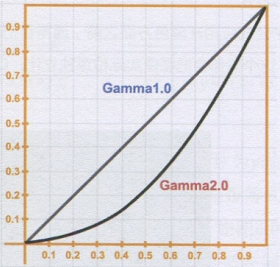
蓝色的线条表示Gamma输出为1.0,红色的线条表示Gamma输出为2.0。
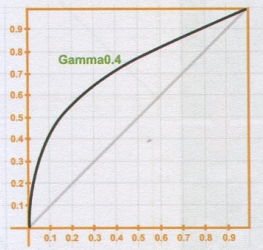
当所有的Gamma值都小于1.0时,得到的结果也会越大,也就是相反的曲线形状。当我们将Gam值调整为0.4:
0.000.4=0
0.250.4 = 0.5743...
0.500.4 = 0.7578....
0.750.4= 0.8913....
1.000.4= 1.00
在这之前,我们的最小值和最大值都保持在0~1之间没有改变,所有其他的值都有了较大的改变,如图所示。
现在如果我想要把两个Gamma操作合并呢?例如上面的函数Gamma0.4外再进行--个Gamma3.0的操作会得到什么样的结果呢?根据指数法则我们知道,在一个指数函数外再加一个指数,就是把两个指数相乘:
(xa)b=xab
合并一些Gamma操作其实就是简单的乘法操作。当Gamma 为2.0,我们想要通过一种 方式来使最终的结果为Gamma等于1.0。很明显我们需要另外的power指数函数,也就是什么值乘以2能得到1呢?答案就是12=0.5,我们称之为倒数(或是乘法互逆),如果两个数相乘的结果为1,那么这两个数就互为倒数。
由此得出,如果想要把- 个经过Gamma校正的图像恢复为linear [线性],便需要在此Gamma基础上再乘以一个当前Gamma的倒数即可:
linear output = input1/current Gamma
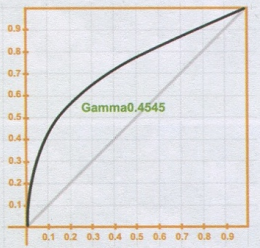
这也就解释了为什么当显示器对画面进行了Gamma2.2的操作,这是为了使图像恢复正常的线性显示,我们需要再为图像进行- 次Gamma 0.4545的操作,2.2 X0.4545= 1.0,如图所示。
通过上面的学习,我们知道Gamma其实就是一条曲线,其背后的运算为指数运算,并且Gamma值为L.0时的曲线为Linear [线性]曲线。
为什么要学习这些呢?因为早期CRT显示器显示的问题导致图像显示较暗。这种好像电视的色彩空间YUV一样的历史遗留问题,直接导致现在的图像在拍摄后其Gamma便不是Linear [线性]。
Gamma的由来其实与我们所使用的电脑的显示设备有很大的关系。由于早期的CRT显示器使用的是电子枪发射电子束到荧光屏幕上,但是屏幕上显示的亮度和实际的亮度信号并不是1:1的,而存在一种度失真。假设输入的是黑白信号,这种失真将使被显示的图像中间区域偏暗,从而觉得图像整体比原始图像偏暗;如果输入的是彩色信号,这种失真除了使显示的图像偏暗以外,还可能会造成图像的色调发生偏移。Gamma伽马校正就是用来解决这一问题的。
通过对原始输入的信号进行伽马校正,提高其中间调区域来恢复其原始亮度。对于CRT显示器,由于品牌不同,其技术水平也有所不同,但一般来说,Gamma伽马校正值就是2.2。这也是Gamma22的由来。
Notice :只有CRT显示器存在亮度信号失真这种问题,现在的液晶显示器并不存在这种问题。
下图所示为Sony显示器的Gamma伽马曲线,图上的曲线表示的就是Sony显示器未经校正的Gamma伽马曲线,x轴为输入的亮度信号,y轴为屏幕显示的亮度(单位为cd/m2流明度)。
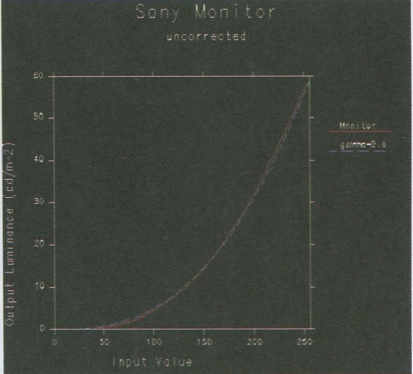
我们可以看到输入值与输出值并不是一-对应的,而存在-条凹陷的曲线,这会使输出图象的亮度明显偏暗。如果想要解决这个问题,可以通过为输入值应用--条对应的倒数曲线,这样便可以使最终的显示结果恢复正常。
下面一组图像就是为了说明Gamma曲线对图像亮度所产生的影响,如图所示。
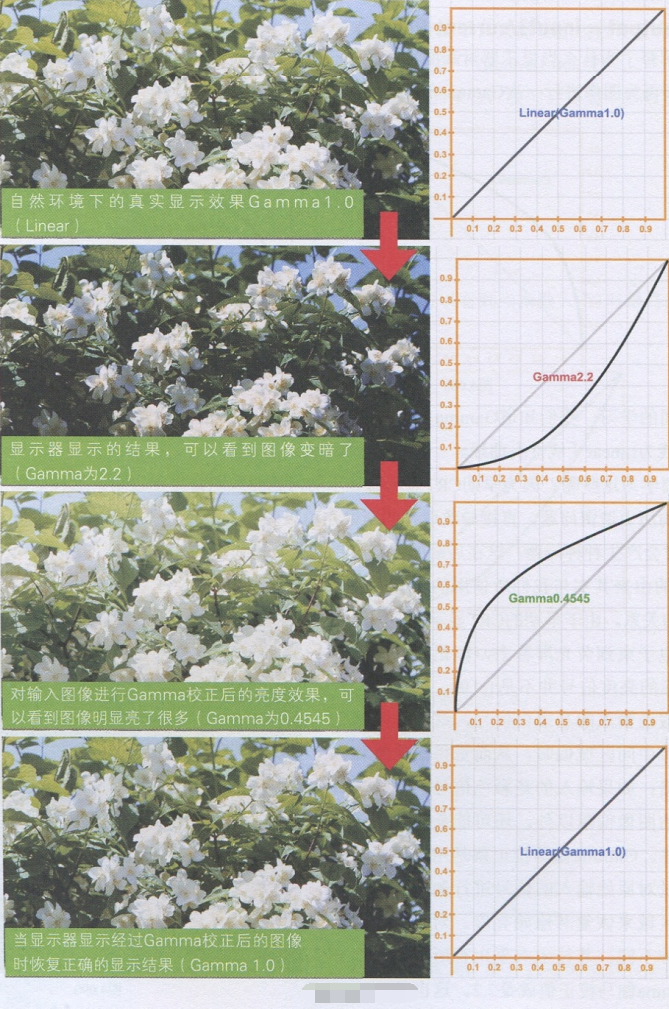
由上面的原理我们知道,所有图像在真实环境下其Gamma曲线都是1.0,可以显示正确的明暗效果,但当使用显示器进行显示时,便会显示为比我们肉眼所看到要暗的图像,因为图像进行了一个Gamma 2.2的调整。所以为了解决这个问题,大多数数字图像在产生后就自动加亮了(进行了Gamma04545的反向调节),这样显示在显示器上时,其实进行了如下运算:
Gamma 2.2 x Gamma 0.4545 = Gamma 1.0
这样便把Gamma恢复成了1.0的正确显示结果。对于大多数普通用户来说,这确实是一件好事,它使我们看到了正确的图像效果,不需要我们手动去做任何亮度调节处理。Gamma的调整确实方便了普通用户,但对于我们制作人员来说却变成了一一个问题。
如果一张图像其对于场景的亮度描述不是线性的,一旦我们对其进行操作,或是把它同其他的图片进行合成操作,便会得到错误的颜色结果,我们将不同Gamma值的图像进行合成操作时,会得到不同的Y值,也就是不同的亮度值,如图所示。
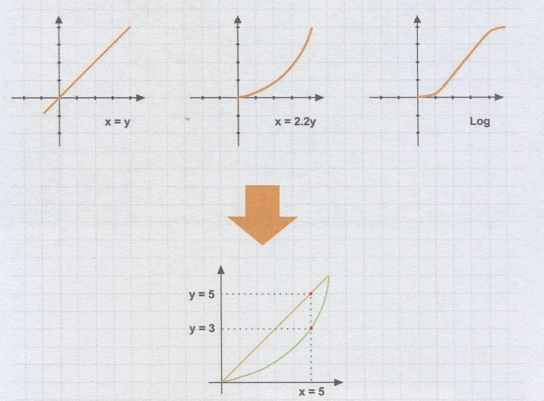
把几种不同坐 标曲线的图像进行合成操作,因为每个坐标系的曲线不同,同一个X如等于5,那么代入不同的坐标系,得到的Y也不相同。
如何来解决这个 问题呢?聪明的小伙伴可能已经想到了,那就是把所有图像都转换成Linear [线性,这样一来,所有的X就都等于Y。这便提醒我们建立一个正确地使用Gamma的工作流程,把所有的工程文件都转换为线性状态进行存储和操作。很多软件并没有把Gamma的校正作为默认操作来处理,好在ENike在这方面进行了自动操作。
热门课程
专业讲师指导 快速摆脱技能困惑相关文章
多种教程 总有一个适合自己专业问题咨询
你担心的问题,火星帮你解答-
专注于游戏原画美术培训的学校,将技术和艺术完美地融合在一起,助力学生们追逐梦想,筑梦游戏美术。
-
深入解析Maya角色建模的方法和技巧,对于想要学习游戏角色建模的朋友们,本文提供了一些具有参考价值的训练方向和建议。
-
了解影视剪辑专业培训的重要性,在火星时代教育中利用专业的课程和最新的技术,你也可以成为领域内的佼佼者。
-
深入了解影视后期设计的知识和技巧,探索未来的影视产业。火星时代教育专业培训,引领创新潮流。
-
入门级CG动画制作培训班,一篇文章让你了解CG动画制作的魅力,以及详细课程内容,真实评价。
-
了解Axure课程的重要性,以及通过火星时代教育的专业Axure短期培训课程如何提升您的设计技能。

 火星网校
火星网校
















